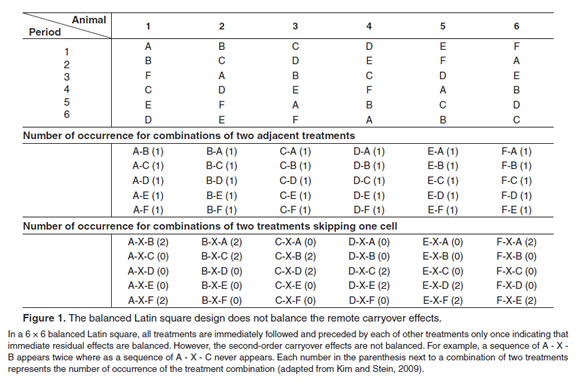
For example in the above 3 x 3 example square treatment B follows A three times in the rows. A plant biologist conducted an experiment to compare the yields of 4 varieties of peanuts A B C D. balanced latin square design.
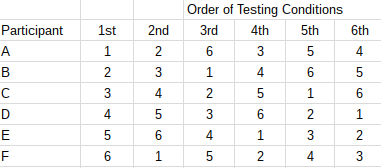
Balanced Latin Square Design, Carryover balance is achieved with very few subjects. One common way to assign treatments to subjects is to use a Latin square design. In a 6 6 balanced Latin square all treatments are immediately.
 Within Subject Study Designs Latin Square Paasp Network From paasp.net
Within Subject Study Designs Latin Square Paasp Network From paasp.net
Three treatment groups A B C three periods period 1 period 2 and period 3 and six sequences ABC BCA CAB CBA ACB and BAC. Williams row-column designs are used if each of the treatments in the study is given to each of the subjects. A plant biologist conducted an experiment to compare the yields of 4 varieties of peanuts A B C D.
This balanced Latin Square is a commonly used instrument to perform large repeated measured designs and is an excellent compromise between maintaining validity and practicality.
Three treatment groups A B C three periods period 1 period 2 and period 3 and six sequences ABC BCA CAB CBA ACB and BAC. You can also generate balanced latin squares directly from your code by copying the following function. This balanced Latin Square is a commonly used instrument to perform large repeated measured designs and is an excellent compromise between maintaining validity and practicality. A balanced 6 6 Latin square design using this method is illustrated in Figure 2. Designs balanced for the effect of the two preceding treatments and their interactions. In a 6 6 balanced Latin square all treatments are immediately.
Another Article :

The systemic method balances the residual effects when a treatment is an even number. Because the designs are balanced all treatment di erences have the same estimated variance. Latin square designs allow for two blocking factors. Since not all the treatments can be compared within each block a new class of designs called balanced incomplete. For instance if you had a plot of land the fertility of this land might change in both directions North – South and East – West due to soil or moisture gradients. Taino Symbolism English Booklet For Pdf Scribd Symbols Booklet Indian Tattoo.

Latin squares have been widely used to design an experiment where the blocking factors and treatment factors have the same number of levels. 3112 Latin Square Example Peanut Varieties Example. Treatments appear once in each row and column. For instance if you had a plot of land the fertility of this land might change in both directions North – South and East – West due to soil or moisture gradients. The systemic method balances the residual effects when a treatment is an even number. Medieval Dietetics The Theory Of Humours 4 Temperaments Greek Medicine Medical Knowledge Humor.
Latin square designs allow for two blocking factors. For example a study design with 3 treatment groups will have the following assignments. Because the designs are balanced all treatment di erences have the same estimated variance. The systemic method balances the residual effects when a treatment is an even number. What is a Balanced Latin Square Design. A Program For Making Completely Balanced Latin Square Designs Employing A Systemic Method.
Latin square designs are often used in experiments where subjects are allocated treatments over a given time period where time is thought to have a major effect on the experimental response. Latin square designs are often used in experiments where subjects are allocated treatments over a given time period where time is thought to have a major effect on the experimental response. The systemic method balances the residual effects when a treatment is an even number. For example in the above 3 x 3 example square treatment B follows A three times in the rows. It follows C zero times. A Program For Making Completely Balanced Latin Square Designs Employing A Systemic Method.
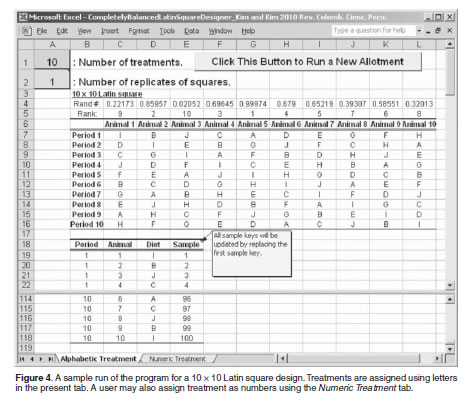
The systemic method balances the residual effects when a treatment is an even number. A design can be developed from a set of n-l mutually orthogonal Latin squares obeying certain restrictions. In this example treatments A to F are ordinarily assigned in the first row animal. For var i 0. Since not all the treatments can be compared within each block a new class of designs called balanced incomplete Latin squares BILS is proposed. A Program For Making Completely Balanced Latin Square Designs Employing A Systemic Method.

Latin Square Design 21 Latin square design A Latin square design is a method of placing treatments so that they appear in a balanced fashion within a square block or field. LATIN SQUARE DESIGN LS Facts about the LS Design -With the Latin Square design you are able to control variation in two directions. For var i 0. A balanced 6 6 Latin square design using this method is illustrated in Figure 2. A Williams design is a generalized latin square that is also balanced for first order carryover effects. Natural Phenomena Integrates The Physical And Social Conditions That Frame The Project The Form And Special Arrangement Natural Phenomena New Museum Physics.

There are other variations of counterbalanced measures designs. There are six Williams squares possible in case of four treatments. Since not all the treatments can be compared within each block a new class of designs called balanced incomplete. Constructing the Williams squares is not a randomization yet. For example a study design with 3 treatment groups will have the following assignments. Latin Square Design Definition And Balanced Latin Square Algorithm Statistics How To.

The systemic method balances the residual effects when a treatment is an even number. 3112 Latin Square Example Peanut Varieties Example. Williams row-column designs are used if each of the treatments in the study is given to each of the subjects. For some experiments the size of blocks may be less than the number of treatments. There are six Williams squares possible in case of four treatments. Pin On Good Looks.

Treatments appear once in each row and column. Latin square designs allow for two blocking factors. There are six Williams squares possible in case of four treatments. A Williams design is a generalized latin square that is also balanced for first order carryover effects. For example a study design with 3 treatment groups will have the following assignments. Within Subject Study Designs Latin Square Paasp Network.

A balanced latin-square design is a modified version of thelatin-square design. -Treatments are arranged in rows and columns -Each row contains every treatment. A design can be developed from a set of n-l mutually orthogonal Latin squares obeying certain restrictions. A Williams design is a generalized latin square that is also balanced for first order carryover effects. In other words these designs are used to simultaneously control or eliminate two sources of nuisance variability. Rainbow Squares Black By Lorna Hooper Rainbow Rainbow Wallpaper Square Wall Art.
Latin Square Design 21 Latin square design A Latin square design is a method of placing treatments so that they appear in a balanced fashion within a square block or field. For some experiments the size of blocks may be less than the number of treatments. Replicates are also included in this design. Carryover balance is achieved with very few subjects. With the Latin Square listed below we can easily construct the crossover design with treatments periods and sequences. Latin Square Design Definition And Balanced Latin Square Algorithm Statistics How To.

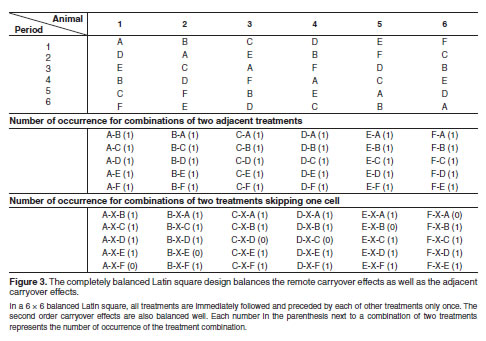
In a 6 6 balanced Latin square all treatments are immediately. A balanced 6 6 Latin square design using this method is illustrated in Figure 2. An advantage of this design for a repeated measures experiment is that it ensures a balanced fraction of a complete factorial that is all treatment combinations represented when subjects are limited and the sequence effect of treatment can be considered to be negligible. Treatment peanut variety Column. Two squares for eight subjects. Latin Square Design Definition And Balanced Latin Square Algorithm Statistics How To.

-Each column contains every treatment. A plot of land was divided into 16 subplots 4 rows and 4 columns The following latin square design was run. Latin square designs are often used in experiments where subjects are allocated treatments over a given time period where time is thought to have a major effect on the experimental response. An advantage of this design for a repeated measures experiment is that it ensures a balanced fraction of a complete factorial that is all treatment combinations represented when subjects are limited and the sequence effect of treatment can be considered to be negligible. If the number of treatments to be tested is even the design is a latin square otherwise it consists of two latin. A Program For Making Completely Balanced Latin Square Designs Employing A Systemic Method.

There are other variations of counterbalanced measures designs. The systemic method balances the residual effects when a treatment is an even number. In a 6 6 balanced Latin square all treatments are immediately. A Latin square is a block design with the arrangement of v Latin letters into a vv array a table with v rows and v columns. For example a study design with 3 treatment groups will have the following assignments. Within Subjects Vs Between Subjects Designs Which To Use.

-Treatments are arranged in rows and columns -Each row contains every treatment. It follows C zero times. A systemic method for balanced Latin square designs The systemic method balances the residual effects when a treatment is an even number. Latin square designs allow for two blocking factors. Designs balanced for the effect of the two preceding treatments and their interactions. New Balance Logo Logok New Balance Logo Corporate Id.